应变分析的改善

干扰对采集精度有重大影响，能够切断干扰的滤波器特性与性能尤为重要。下面对切断动态应变中发生的高频干扰的滤波器进行说明。另外，还介绍表示应变片灵敏度的应变系数与自动平衡。

低通滤波器

动态应变采集中为切断不必要的高频率干扰，设定低通滤波器是必不可少的。动态应变放大器的滤波器一般使用贝塞尔滤波器或巴特沃斯滤波器。

瞬态特性优异且过冲及振铃小，因此在模拟信号等重视波形的用途上适用贝塞尔滤波器。

表示能力时，输入相隔1个八度音阶的频率时的衰减率用dB表示。
提升滤波器的次数后虽然衰减率得到改善，但过冲与振铃会变大，因此仅提升数次左右。

八度音阶（octave）表示频率为2倍。
另外，衰减率表示
-3 dB=约0.7倍
-20 dB=约0.1倍
-30 dB=约0.03倍
，屏蔽频率设为5 kHz时，表示
在-30 dB/oct输入10 kHz1 V后将成为0.03 V以下。

在应变采集中有个重要的值就是“应变系数”。
首先，表示应变片的输出电压大小。
下图为单应变片法的接线图。
应变为零时，由于处于平衡状态，电压e为0 V的内容已在上文说明过。
发生了应变时，电压e值由下式表示。

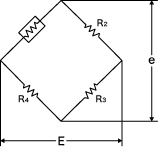
e=1/4 × E × Ks × ε…（1）

E：电桥电源电压Ks：应变系数ε：应变量
同时，不限于单应变片法的通用公式如下。

e=1/4 × Ks（ε1-ε2+ε3-ε4）E

前项公式（1）中的“Ks”就是称为应变系数的比例常数。
真实应变系数一般固定为2.0。
（实际应变系数存在偏差，在每个箱子记载了应变系数）
而且，电桥电源一般为2 V。
其原因一算便知。先在公式（1）中代入数值。

e=1/4 × E × Ks × ε …（1）
↓（代入E=2 V、Ks=2.0）
e=1/4 × 2 × 2 × ε=ε

如此应变量即可通过直接读取来采集。
这是很方便的方法。

应变片的应变系数以2.00作为基准制作而成，实际偏差在1.9到2.2左右。
应变记录仪的应变系数固定为2.00，因此应变系数相差0.1，则误差率约为5％。
因此，需要使用应变片箱子上记载的应变系数K，通过记录仪的比率补正功能进行补正。

ε₀=ε × 2.00/K

ε₀：真实应变量 ε：采集的应变量
使用应变系数为2.09的应变片时

ε₀=ε × 2.00/K=ε × 2.00/2.09=0.957 × ε

开始应变采集前，请务必进行自动平衡调整。接触采集目标物时，应变片将发生细微的应变。
消除此时的应变量，将无负载状态的采集值设为0的作业就是自动平衡。

希望进一步了解应变的人士！

全面汇总了应变采集的基础知识、实践、诀窍！