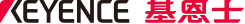数值孔径（N.A.）

数值孔径或N.A.是一个表示镜头分辨能力的数值，由以下等式定义。

n：观察介质的折射系数 [如n（空气）= 1]
θ：光轴和镜头有效直径内最外部的光形成的角度

N.A. = n * sin θ

镜头的分辨率是由N.A.决定的，但是衍射的作用不可忽视。使光像波浪般分散的现象称为“衍射”。由于衍射的原因，即使分辨率最高的镜头也不能把焦点集中在一点上，导致焦点呈圆盘形状。尺寸最小的可分辨的光斑被称为“艾里斑”。艾里斑的半径用以下公式表示。

λ：光的波长
N.A：数值孔径
0.61：固定数值

r = 0.61 * λ/N.A.

这个公式得出的数值就是“分辨率”。根据这个公式，数值孔径（N.A.）越大，艾里斑的半径越小。因此，镜头的数值孔径（N.A.）越大，可分辨的特征越小，图像就越清晰。