电荷与库仑定律

让我们来对发电的基础——电荷，进行深入解析。下面将从电荷的定义等基础知识开始，到利用库仑定律计算电荷量的方法，进行详细说明。

何谓电荷

电荷是指带电物体所具有的电量。电子多于质子时为-，电子少于质子时为+。电荷的符号为Q，单位以C（库仑）表示。将2个电荷量设为Q1、Q2，距离设为r[m]，两个电荷间的作用力设为F[N]时，库仑定律如以下公式所示。

在一般介质中，如下所示。（但，εs为介质的相对介电常数。）

带电物体彼此靠近时，产生相同极性的静电会相互排斥，而相反极性的静电则相互吸引的作用力。
此时产生的电荷力被称为“库仑力”（单位为[N]），相应电荷量与力的关系，可通过“库仑定律”来表示。

大小无法测量的极小物体带有的电荷称为点电荷，当在真空环境下电荷量Q[C]的点电荷A与电荷量Q’[C]的点电荷B靠近，距离为r[m]时，利用库仑定律计算静电力F，就会发现其与B和A的距离r[m]的平方成反比，且与A的电荷量和B的电荷量之积成正比。

作为比例常数，ε₀是被称为真空介电常数（8.85 x 10^-12[F/m]：法米）的常数。
此库仑力在2个电荷为相同极性时就是排斥力，极性相反时则是吸引力，用重力加速度9.8[m/s²]相除即可得到[kg]。

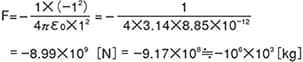
2个点电荷1[C]与-1[C]的距离为1[m]时的静电力(F)如公式所示。

据此计算，相当于约100万吨重的作用力，即，将100万吨的重物提起的力。因1库仑[C]的单位过大，实际上使用使1[m]的四方形高分子薄膜摩擦带电时的带电量，约为10^-5[C]。

据传，古希腊哲学家泰勒斯（Thales BC.640-546年）发现了库仑定律，但是，将这个理论正式规定为定律的是库仑（1739-1806年），并于1785年发表。