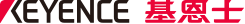静电容量计算方法
至此,我们学习了电荷及电场。表示能够蓄积多少电荷的就是静电容量。下面将从静电容量的基础知识至计算方法进行详细说明。
何谓静电容量
静电容量是表示电容器等能够蓄积多少电荷的量,也称为电容量。
带电体的电位与带电量具有如下比例关系。
Q=CV[C]
这个比例常数C被称为静电容量,单位用[F:法拉]表示。
电荷量为1 C,电位差为1 V时的容量为1 F。但是,由于这个单位过大,并不实用,因此一般使用表示1 F的100万分之1(10-6)的μF(微法)及表示1 F的1兆分之1(10-12)的pF(皮法)。
1 F=106 μF=1012 pF
图为将静电容量比作装入容器的水来进行说明的图例。
将装入容器的水量视为电荷量,将水位视为电位,将容器底部的面积视为静电容量。
当相同量的水装入底部面积小的容器时,水位立即上升,但装入底部面积大的容器时,水位则较少上升。换言之,若将带电体视为蓄积电荷的容器,静电容量即表示容器的大小(容量)。
此例中的水与电子的区别在于,水从水位高的地方流向低的地方,最终导致水位相等,而电子则使释放电子侧的电位上升,并使吸收电子侧的电位下降。这意味着前者带正电,后者带负电。

静电容量的计算
计算静电容量时,可根据带电体的大小、形状及周围的状况,通过以下公式计算。
球形导体时
向半径为a[m]的球状导体赋予电荷[Q]时的表面电位为
V=Q/4πε0a[V],
静电容量为
C=Q/V=4πε0a[F]
。
平行导体板时
如图所示,2块导体板为平行状态,面积为S[m2],间隔为d[m]时,分别赋予+Q、-Q电荷,此时电极间存在的电场强度为

(电荷密度σ=Q/S)
,电极间的电位差[V]为
V=Ed=dQ/Sε0
由此,静电容量如下。

另外,导体板间存在绝缘体时,(绝缘体的相对介电常数)静电容量为以下公式所示。


【例1】带电体的静电容量
如图所示,多个导体接近1个导体并接地时,各个导体的静电容量之和即为该物体的静电容量。

【例2】绝缘体的静电容量
绝缘体薄膜的背面紧贴着导体板并接地时。
例如,厚度d[m]的绝缘体薄膜(相对介电常数)紧贴着已接地的导体板,薄膜表面存在Q[C/m2]的电荷时。
薄膜背面出现与紧贴着的导体板极性相反而数量相等的电荷。
此时电荷分布如图所示,呈现出与2块电荷密度为σ的平行板带电时相同的状态。

该状态下的绝缘体表面电荷Vs如下。

【例3】绝缘体薄膜厚度不同时
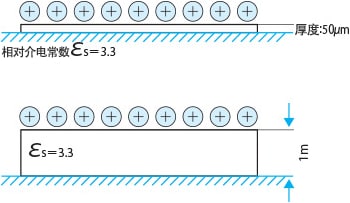
如下图所示,聚酰亚胺薄膜(厚度100[μm]、相对介电常数=3.3)紧贴着接地导体板,且表面电荷密度设为σ=1 x 10-5[C/m2]时,表面电位为

相同条件下,薄膜厚度为1[mm]时,

薄膜厚度不同时,即使相对介电常数及电荷密度相同,表面电位仍出现较大差异。